Umeyama算法是在点云配准中常用的一个算法,在三维点云配准中通常需要三对以上的点构建对应关系后解算变换矩阵,pcl点云库中使用Eigen库中的Eigen::umeyama进行求解。
Least-Squares Estimation of Transformation Parameters Between Two Point Patterns
两组点集模式下变换参数的最小二乘估计
算法目的
设空间中有两个点集X和Y(X和Y可能是完全相同的两个点集也有可能是从点集中选取的部分点构成的点集),点集X和点集Y处于不同的局部坐标系当中。此算法的目的是通过计算旋转矩阵R、平移矩阵s和缩放系数t,并作用域点集Y上得到Y1,使得X和Y1中每个点的距离差的平方和最小。
计算步骤
根据两个点集的相似变换建立方差

首先计算两个点集的均值:


然后计算两个点集的方差:


其次还要计算X和Y点集的协方差:

对协方差进行SVD分解,记作UDVT(D = diag(di),d1 >= d2 >= ... >= dm >= 0),其中S表达式为如下方式:

那么相似矩阵中的参数可以表示为如下表达式:
R = USVT
t = uy - cRux
c = tr(DS) / δx2
现在介绍Eigen::umeyama的用法
Umeyama.h中的定义如下:
1 | umeyama(const MatrixBase<Derived>& src, const MatrixBase<OtherDerived>& dst, bool with_scaling = true) |
由于结果以相似矩阵的形式进行存储,所以需要事先定义一个4*4的矩阵:
1 | Eigen::Matrix<double, 4, 4> Result; |
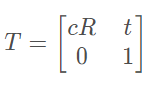
然后定义两个点集用于存储源点云X和目标点云Y的数据(数量为n):
1 | Eigen::Matrix<double, 3, Eigen::Dynamic> X(3, n); |
最后通过umeyama算法得到结果:
1 | Result = Eigen::umeyama(X, Y, false); |
__END__
